杨辉三角简介

杨辉三角，也称为帕斯卡三角形，是一种在数学中广泛使用的三角形结构。它以数学家杨辉的名字命名，最初用于二项式定理的计算。杨辉三角中的每个数都是其上方两数之和，这个性质使得它在组合数学、概率论和计算机科学等领域有着广泛的应用。

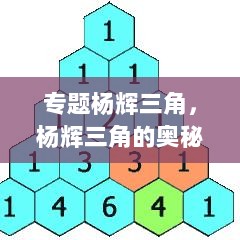
杨辉三角的结构

杨辉三角的每一行都代表了一个二项式展开式的系数。第一行是单个项的系数，即1。从第二行开始，每一行的第一个和最后一个数都是1，中间的每个数都是上一行相邻两个数的和。这种结构可以通过递推关系来表示：C(n, k) = C(n-1, k-1) + C(n-1, k)，其中C(n, k)表示从n个不同元素中取出k个元素的组合数。

杨辉三角的性质

杨辉三角具有许多有趣的性质，以下是一些常见的：

• 对称性：杨辉三角关于其中心线对称。

• 斐波那契数列：在杨辉三角的第n行中，第n个和第n+1个数分别是斐波那契数列的第n-1项和第n项。

• 二项式定理：杨辉三角的每一行对应于二项式定理的一个展开式。

  

• 整数解：杨辉三角中的每个数都是整数，并且除了第一行和最后一行外，每个数都是偶数。

杨辉三角的应用

杨辉三角的应用领域非常广泛，以下是一些例子：

• 组合数学：杨辉三角可以直接用于计算组合数，这在解决概率问题、密码学、计算机科学中的算法设计中非常有用。

• 概率论：在概率论中，杨辉三角可以用来计算独立事件的概率乘积，以及某些随机变量的分布。

• 计算机科学：在计算机科学中，杨辉三角可以用来生成排列组合、构建哈希表、优化算法等。

• 数学教育：杨辉三角是数学教育中的一个重要工具，可以帮助学生理解组合数学、概率论等概念。

杨辉三角的历史

杨辉三角的历史可以追溯到中国的古代数学。最早出现在《九章算术》中，后来在《孙子算经》和《释名》等书籍中也有记载。尽管杨辉三角在西方数学中较为晚出，但它的影响力和应用范围却非常广泛。在西方，杨辉三角的研究始于17世纪的法国数学家帕斯卡，因此也被称为帕斯卡三角形。

杨辉三角的现代研究

在现代社会，杨辉三角的研究依然活跃。数学家们不断探索其新的性质和应用，以下是一些现代研究领域的例子：

• 数论：杨辉三角中的数可以用来研究数论中的某些问题，如模运算、同余等。

• 图论：杨辉三角可以用来解决图论中的某些问题，如网络流、匹配问题等。

• 量子计算：在量子计算领域，杨辉三角的概念被用来构建量子逻辑门和量子算法。

结论

杨辉三角是一种简单而强大的数学工具，它的结构和性质在多个学科中都有着广泛的应用。通过对杨辉三角的研究，我们可以更好地理解数学中的许多概念，并将其应用于实际问题中。杨辉三角的历史和现代研究都证明了它在数学和科学中的重要地位。